2017/6/9 駒形圭祐
1-1よく使われるn進数
コンピュータでよく使われるのは2進数と8進数と16進数。
2進数の2という数字は「桁が進む数」を表す。
8進数と16進数も基本同じ。
基数と桁の重みについて
基数→n進数のnにあたる数字。
例)2進数なら2 16進数なら16
重み→1、10、100のように1が1桁左に行くと、
基数nの(桁数-1)乗をおこなった数字になる。
例)基数2の場合
1桁目→2^0=1 2桁目→2^1=2
3桁目→2^2=4 4桁目→2^3=8
小数点以下第一位→2^-1=2分の1
小数点以下第二位→2^-2=4分の1
1-2 基数変換
①n進数から10進数への基数変換
各桁の数に重みを掛けた数を計算しそれを合計する。
例)2進数 1101.011 を10進数にする。
8+4+0+1+0+0.25+0.125なので
2進数1101.011を10進数にすると13.375になります。
②10進数からn進数への基数変換
■整数部
→基数で商が0になるまで割り算した余りを下から上位ビットに入れる。
■小数部
→基数で小数部が0になるまで掛け算した整数部分を上位ビットに入れる。
例)13.375を2進数に変換
●整数部 13/2=6余り1 6/2=3余り0 3/2=1余り1 1/2=0余り1
余りを下から入れていくと1101
●小数部 0.375*2=0.75 0.75*2=1.5 0.5*2=1.0
整数部分を入れていくと011
なので1101.011になります
③2進数と8進数と16進数の基数変換
まず前情報として、
8進数は2進数3桁で表せます。
なぜなら2進数3桁で7まで表せるから。2進数111=7。
16進数も同じように2進数4桁で表せます。
なぜなら2進数4桁で15まで表せるから。2進数1111=15
なので、もし2進数を8進数に直したいのなら2進数を
3桁に区切ればその区切った桁一つ一つが8進数の一桁にあたります。
例)2進数1011.01を8進数にする。
まず、2進数を3桁ずつに区切ります。
(0が足りないところは付け足してOKです。)
↓()は0を付け足したところ
2進数 (00)1 011 . 01(0)
8進数 1 3 2
それぞれを10進数にすると1 3 2になるので
2進数1011.01を8進数にすると13.2になります。
16進数も同じように4桁に区切り同じように計算します。
2進数1011.01を16進数にするとD.4になりますのでやってみてください。
また、8進数13.2と16進数D.4を10進数にしてみて
同じ数になるか確かめてみて下さい。
※n進数から10進数のヒント
→その桁の数字*(基数^桁数-1)を足し合わせる。
2-1 2進数の足し算と引き算
コンピュータは足し算しかできません。
なので、引き算をするには負の数が必要です。
コンピュータで負の数を表すのには2の補数を使います。
2の補数の求め方
①ビットの0と1を反転
②その数値に1を加える
例)2進数3の補数(1101)を求める。
※説明のため4ビットの領域を想定
2進数の3 0011
①ビットの反転→1100
②1を加える→1101
●具体的な引き算の流れ
例)5-3を行う場合
0101-0011 =0101+(-0011)
=0101+1101←3の補数
=10010←桁あふれしたビットを切り捨てると答えの2になる。
2-2 シフト演算と2進数のかけ算・割り算
2進数のビット列を左右にずらす操作をシフト演算と呼びます。
ビット列を左にnずらす→2^n倍される。
ビット列を右にnずらす→1/2^nされる。
シフト演算をする際に符号を考慮するかどうかで2つのシフト操作がある。
符号を考慮しない→論理シフト
符号を考慮する→算術シフト※符号ビットが0→正の数 1→負の数
●左論理シフトのやり方
例)00101100(10進数で44)を4倍(2^2倍)する
①ビット列を左に2ずらし、はみ出たビットを削除。
②空いたスペースを0で埋める。
001011**→101100(10進数で176)
※もしビット列をずらした際に1がはみ出たらオーバーフロー(後述)する。
 ●右論理シフトのやり方
●右論理シフトのやり方
例)00101100(10進数で44)を1/4(1/2^2)する
①ビット列を左に2ずらし、はみ出たビットを削除。
②空いたスペースを0で埋める。
**101100→001011(10進数で11)
※もしビット列をずらした際に1がはみ出たら余り。
●左算術シフトのやり方
例)11100100(10進数で-28)を4倍(2^2倍)する
①最上位ビット(符号ビット、この例では8ビット目)を
除いたビット列を左に2ずらし、はみ出たビットを削除。
②空いたスペースを0で埋める。
1110100**→1001000(10進数で-112)
※算術シフトの場合符号ビットと異なるビットがはみ出ると
オーバーフローする。
●右算術シフトのやり方
例)11100100(10進数で-28)を1/4(1/2^2)する
①最上位ビット(符号ビット、この例では8ビット目)を
除いたビット列を右に2ずらし、はみ出たビットを削除。
②空いたスペースを符号ビットと同じビットで埋める。
1**00100→11111001(10進数で-7)
コンピュータのかけ算・割り算の考え方
●コンピュータのかけ算の考え方
×2、×2^2→×4、×2^3→×8などはシフト演算で
できます。でも×3や×7はどうするかについてです。
結論としては2^n同士の足し算に置き換えます。
例)
×3→2^1+2^0
×7→2^2+2^1+2^0
●コンピュータの割り算の考え方
前提として割り算がどういったものかを考える。
例えば20÷5がどういうものかと考えると
20は5ずつに4回分けられることを意味します。
これは言い換えると、20から5を4回引くことができる
ということになります。
なので2^nの引き算に置き換えます。
2-3 小数点を含む数の表し方
コンピュータでは小数点を表す方法が2つある。
1、固定小数点数→ビット列のどの位置に小数点があるかを
暗黙的了解として扱う表現方法。
例)
●8桁のビット列で頭から5ビットを整数とする
→00000. 000
整数部 小数部
●最下位ビットの右側を小数点とする
→整数部のみを表せるようになる
2、浮動小数点数→指数表記を用いて数値を扱う表現方法。
表し方

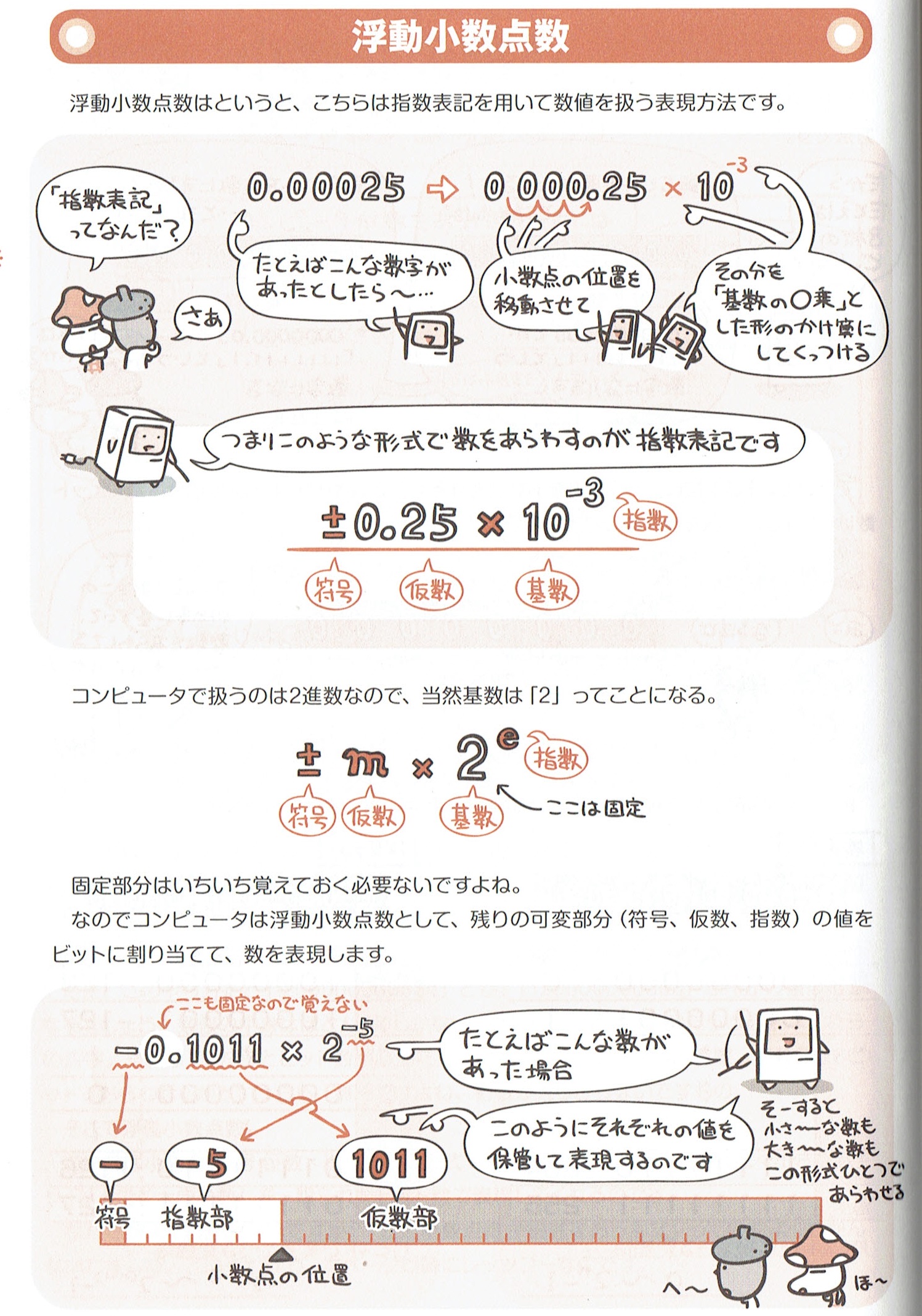
正規化のやり方

よく使われる浮動小数点数の形式



2-4 誤差
誤差とは、実際の数値とコンピュータ内部で表現できる数値との間に
生じたずれを、誤差と呼びます。
●けたあふれ誤差
演算した結果が、コンピュータの扱える最大値や最小値を超えることによって生じる誤差
最大値を超えてしまうことをオーバーフロー
最小値を超えてしまうことをアンダーフロー
*アンダーフローはマイナスの数字ではなく0.000000000000000000000…000000000000001のような数字がなる。
●情報落ち
絶対値の大きな数と絶対値の小さな値の加減算を行った時に、
絶対値の小さな値が計算に反映されないことによって起こる誤差
例)仮数部を4で表す浮動小数点数があったとする。
次の足し算をする0.1234×10^4+0.1234×10^-4
=0.123400001234×10^4
正規化すると0.1234×10^4になり有効桁からはみ出してしまうので
小さな数の方はなかったことになってしまいます。
●打切り誤差
円周率のように延々続く計算処理を、完了まで待たずに途中で打ち切ることによって生じる誤差
●けた落ち
絶対値がほぼ等しい数値同士の差を求めた時に、有効なけた数が
大きく減ることによって生じる誤差
●丸め誤差
表現できる桁数を超えてしまったがために、最小桁より小さい部分について、四捨五入や切上げ、切捨てなどを行うことによって生じる誤差